Related Rates: Angle change as fireworks travel straight upward

1

A student wrote us to ask:
Kindly share the solution for the question below.

A party-goer is standing 30 feet way from the launch site of a large firework. Once the firework ignites, the shell rises at a constant rate of 130 feet per second. Find the rate of change of the angle between horizontal and the firework, from the perspective of the party-goer, when the angle of view is đťś‹/4.

2

Thanks for asking this question! It’s typical of Related Rates problems, and in fact is quite similar to the problem “Related Rates: Rocket, angle changes” in the “Related Rates: Using a Trig Function” part of our Related Rates page.

Let’s use our usual Problem Solving Strategy, as outlined on that page and in our Blog post:

1. Draw a picture of the physical situation.

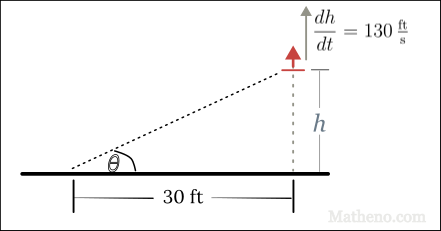
fireworks

2. Write an equation that relates the quantities of interest.
A. Be sure to label as a variable any value that changes as the situation progresses; don’t substitute a number for it yet.

Here, the rocket’s height changes as time passes, so we’ll just call that value h.

The picture immediately suggests a relation between the angle \theta and the height h:

\tan \theta = \frac{h}{30}

Developing that equation is the key to our solution. Learning how to develop such equations just requires practice, and so we have a good number of problems available for you to work through on our Related Rates page.

3. Take the derivative with respect to time of both sides of your equation. Remember the chain rule.

\begin{align*} \dfrac{d}{dt}(\tan \theta) &= \dfrac{d}{dt}\left( \frac{h}{30} \right) \\[8px] \sec^2 \theta \cdot \dfrac{d\theta}{dt} &= \frac{1}{30} \dfrac{dh}{dt} &&& \left[\dfrac{d}{d \theta}\tan \theta = \sec^2 \theta \right] \\[8px] \dfrac{d\theta}{dt} &= \left( \frac{1}{30}\dfrac{dh}{dt}\right) \cos^2 \theta &&& \left[\frac{1}{\sec^2 \theta} = \cos^2 \theta \right] \end{align*}

4. Solve for the quantity you’re after.

We won’t complete the problem for you, but all that remains is to substitute values: The problem tells you that \dfrac{dh}{dt} = 130 \, \tfrac{\text{ft}}{\text{s}}, and asks for the value of \dfrac{d\theta}{dt} when \theta = \dfrac{\pi}{4}. You can finish from here!

We hope that helps. You might want to practice the other problems on our Related Rates page to make sure you know how to solve the various types for yourself and are completely ready for your exam.

Please feel free to write with any other questions that you have, or let us know if any of the steps above don’t make complete sense to you.

For now, thanks again for asking! :grinning: