How far does a car travel while stopping? [kinematics question]

1

A student wrote us with the following (lightly edited):

Hello Matheno!

It’s me again. I am so grateful find you to help me about my question. I have another 2 questions that i want to ask you. I am a little bit curious and i hope that you can teach me with details on this question. Thanks Matheno!

q2 cal
q2 cal1170×314 33.2 KB

We’ve posted the other question as a separate topic.

4

Hello! Thank you for the question!

First, we note the type of problem we are trying to solve, so that we may draw upon the correct “tools” to attack the problem. In this case, because we are dealing with an object that is moving for a certain amount of time and a given constant acceleration, and are being asked to find the displacement of the object, we know we are dealing with a kinematics problem. Knowing this allows us to use the kinematics equations.

Phrases such as “constant deceleration”, “how far does… travel”, and “coming to a complete stop” usually indicate that we are dealing with a kinematics problem.

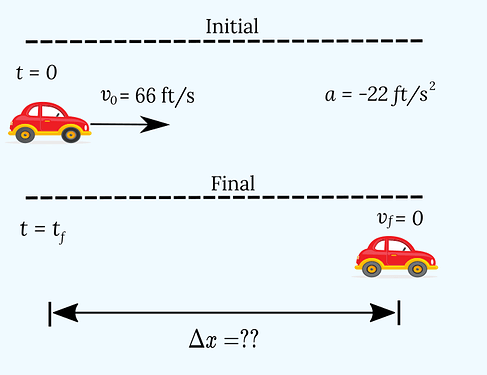
In dealing with kinematics problems, it is generally useful for us to make a rough drawing of the scenario we are given and write down the known and unknown variables. So our drawing might look something like this:

forumDrawing
forumDrawing713×548 33.5 KB

Note how separating the initial and final “states” helps us clearly identify which variables are associated with each state. That is, v_0=66 \text{ ft/s} goes with t=0 while v_f=0 goes with t=t_f.

Now that we have identified the known and unknown variables, as well as designated the quantity we seek, in this case \Delta x, the distance traveled as the car decelerates to a final velocity of 0.

We use the two equations that relate acceleration, displacement, velocity, and time:

\Delta x=v_0 \Delta t+\frac{1}{2}a \Delta t^{2}

and

v_f=v_0+a \Delta t

Note that since t_0 =0, \Delta t = t_f - t_0 becomes t_f. So we can rewrite our equations as:

\Delta x = v_0 t_f + \dfrac{1}{2} a t_f^2

and

v_f = v_0 + at_f

With those two equations, you’ve got all you need: Since you know v_f = 0 and you’re given v_0 and a, you can solve the second equation for t_f and find the moment the car comes to a stop.

Then once you have that value, you can use it in the equation for \Delta x to find the answer to the problem.

Please let us know if you get stuck on any part of this process so we can help out!