In a right angled triangle PQR , angle Q is 90 degrees.PR the hypotenuse is increasing at the rate of 0.5 cm/ sec .side QR is 12 cm … what is the rate of increase of angle QPR when angle QPR is 45 degrees
Welcome to our Forum, @g-hinasolanki, and thank you for your question!
I imagine you’ve already looked at our related rates page, and perhaps even looked at the four types of related rates problems you need to know how to solve. Since this is asking about the rate at which an angle changes, that automatically tells us this is a problem type where we need to use a trig function.
Then, following the first step in our Problem Solving Strategy, we draw a figure, which I trust you did for yourself.
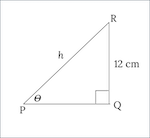
The diagram does a lot of the work for us: we need to related \theta, h, and the unchanging -side that is always 12 cm . . . and from the figure we can see that
\sin \theta = \dfrac{12}{h}
When we take the derivative, then, we have
\cos \theta \cdot \dfrac{d\theta}{dt} = -\dfrac{12}{h^2} \dfrac{dh}{dt}
Now the problem tells us that the hypotenuse, h, is changing at the rate \dfrac{dh}{dt} = 0.5 cm/sec. It also specifies that we want the moment when \theta = 45 degrees. You can find the value of h at that moment from the equation for \sin \theta above, and then you know all of the values to be able to find \dfrac{d\theta}{dt}. (Be aware that your answer will be in rad/sec.)
So that should do it, but if you have further questions please let us know! And we strongly suggest that you work through more of the related rates problems on our page, making sure you do at least a few from each “type” so you’ll be ready for your exams.
For now, thanks again for your question, and please let us know what further questions you have! 
Thank you for your help… I still can’t get it … I’m getting a negative answer and the answer in the book says the angle is increasing at the rate of 1/48 radians per second… please help
Actually, you probably do have it: your negative answer is correct, because as the hypotenuse increases while the opposite side stays the same 12 cm, the angle theta decreases. I made a little Desmos graph to illustrate. (EDIT: This is now a live graph, so you can interact with it right here.)
As you see for yourself, as you move the dot in the upper right more and more to the right so the hypotenuse lengthens, while keeping the triangle’s right side = 12, the angle theta in the lower left gets smaller and smaller, which is what the negative result captures.
Signs are often an issue in related rates problems. As we note elsewhere on our related rates page, and in our blog post, sometimes when the problem explicitly asks for the rate at which an angle decreases, they expect a positive answer since they’ve taken the negative sign into account with the word “decreases.” But not always: sometimes they still want the negative value. (It’s a case where you have to ask your teacher.)
In this case, however, as you wrote it the problem asks for “the rate of increase,” which is indeed negative as the physical situation requires. So I’d say you have it correct (at least the sign), and don’t know what to tell you about your book’s answer.
Thanks very much for trying to make sense of this for yourself. We know it can be challenging to work through issues like this on your own when you’re first learning this stuff, and we appreciate the opportunity to think it through with you!
Please let us know if the negative result makes sense to you, since that’s what we care most about.
Thank you very much for your help… it was very confusing when the answer says increasing in the book solutions and I got a negative answer , tried it in many different ways… but every time got a negative answer
2 Likes